Thể tích khối trụ
Thể tích của khối trụ là không gian mà khối trụ chiếm trong không gian ba chiều. Nó được tính bằng diện tích của đáy nhân với chiều cao của khối trụ. Khối trụ là một hình không gian có hai mặt đáy là hai hình tròn bằng nhau và song song với nhau, và mặt bên là một hình chữ nhật được cuộn tròn lại.
Thể tích của khối trụ thường được biểu thị bằng các đơn vị đo thể tích như cm³, m³, hoặc lít (L), tùy thuộc vào đơn vị của bán kính và chiều cao.
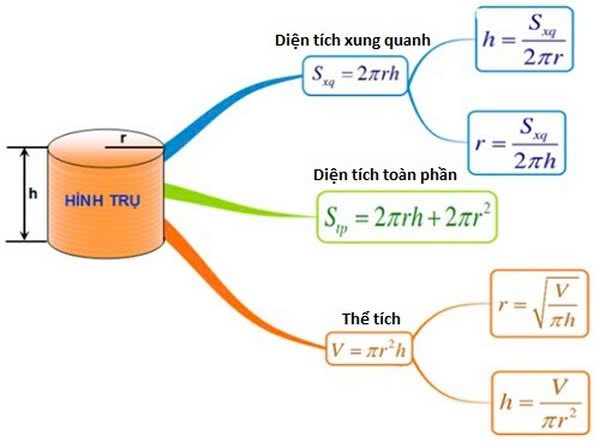
Công thức tính thể tích V của một khối trụ tròn đứng là:
trong đó:
- r là bán kính của đáy hình trụ.
- h là chiều cao của khối trụ.
- π là hằng số Pi (xấp xỉ 3.14159).
Giải thích:
- Bán kính đáy ( r ): Là khoảng cách từ tâm của đáy hình trụ đến mép ngoài của đáy.
- Chiều cao ( h ): Là khoảng cách giữa hai mặt đáy hình tròn của khối trụ, vuông góc với hai mặt đáy.
Công thức thể tích của khối trụTính thể tích của khối trụ cần thiết trong nhiều tình huống thực tế và khoa học. Dưới đây là một số trường hợp cụ thể khi cần tính thể tích của khối trụ:
Kỹ thuật và Xây dựng
- Thiết kế và sản xuất: Trong quá trình thiết kế bồn chứa nước, bình nhiên liệu, hay bể chứa hóa chất, thể tích của khối trụ được tính để biết dung tích chứa của nó.
- Xây dựng cầu đường: Tính toán lượng bê tông cần thiết để đổ vào các trụ cầu tròn hoặc các cấu trúc hình trụ khác.
- Ống nước và cống thoát nước: Tính thể tích của các ống trụ để xác định khả năng thoát nước hoặc vận chuyển chất lỏng.
Khoa học và Nghiên cứu
- Vật lý và Hóa học: Trong nghiên cứu thí nghiệm, thể tích của các khối trụ (như ống nghiệm trụ tròn) được tính để đo lường dung tích chất lỏng hoặc khí.
- Thiên văn học: Thể tích của các thiên thể hình trụ hoặc vật thể không gian hình trụ cũng có thể cần tính trong các nghiên cứu về vũ trụ.
Ứng dụng Công nghiệp
- Lưu trữ và vận chuyển hàng hóa: Tính thể tích của các thùng chứa hoặc xi lanh để xác định dung lượng lưu trữ của các sản phẩm lỏng như dầu, sữa, và hóa chất.
- Sản xuất và đóng gói: Tính toán thể tích của các lon, chai, và hộp đựng để tối ưu hóa quá trình sản xuất và đóng gói sản phẩm.
Trong Giáo dục và Bài tập Học sinh
- Bài toán Hình học: Học sinh thường được yêu cầu tính thể tích của khối trụ trong các bài tập hình học không gian để nắm vững khái niệm và công thức.
- Thi Thực Hành: Đo lường và tính toán thể tích là một phần trong các bài kiểm tra thực hành về hình học và vật lý.
Ứng dụng trong Đời sống Hằng ngày
- Pha chế và Nấu ăn: Tính toán thể tích của các bình đựng để pha chế chính xác đồ uống hoặc công thức nấu ăn.
- Thiết kế nội thất: Đánh giá không gian chứa đựng trong các vật dụng có hình dạng khối trụ như bình hoa, bình chứa gia vị, hoặc các loại hộp đựng.
Việc tính thể tích của khối trụ có rất nhiều ứng dụng thực tế, từ kỹ thuật, khoa học, giáo dục đến các ứng dụng trong cuộc sống hằng ngày.
Dưới đây là một số ví dụ về việc tính thể tích của khối trụ trong các trường hợp thực tế khác nhau:
Ví dụ 1: Tính thể tích của một cái bồn chứa nước hình trụ
Giả sử bạn có một cái bồn chứa nước hình trụ có bán kính đáy là 2 mét và chiều cao là 3 mét. Thể tích của bồn chứa nước này là bao nhiêu?
 Tính thể tích của một cái bồn chứa nước hình trụ
Tính thể tích của một cái bồn chứa nước hình trụVí dụ 2: Thể tích lon nước ngọt
Một lon nước ngọt có dạng hình trụ với bán kính đáy là 3 cm và chiều cao là 12 cm. Hãy tính thể tích của lon nước ngọt này.
 Thể tích lon nước ngọt
Thể tích lon nước ngọtVí dụ 3: Tính thể tích của ống cống thoát nước hình trụ rỗng
Một ống cống thoát nước có dạng hình trụ rỗng với bán kính ngoài là 10 cm và bán kính trong là 8 cm, chiều dài (chiều cao) của ống là 100 cm. Hãy tính thể tích của phần rỗng trong ống.
 Tính thể tích của ống cống thoát nước hình trụ rỗng
Tính thể tích của ống cống thoát nước hình trụ rỗngVí dụ 4: Tính thể tích của cột trụ bê tông
Một cột trụ bê tông có hình trụ với đường kính là 0.5 m và chiều cao là 4 m. Hãy tính thể tích bê tông cần để đổ đầy cột trụ này.
 Tính thể tích của cột trụ bê tông
Tính thể tích của cột trụ bê tôngVí dụ 5: Tính thể tích của một thùng dầu hình trụ
Một thùng dầu hình trụ có đường kính là 1 m và chiều cao là 2 m. Hãy tính thể tích dầu có thể chứa trong thùng này.
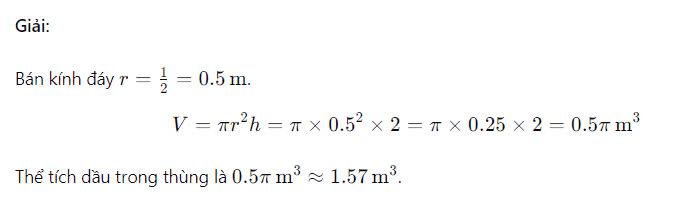 Tính thể tích của một thùng dầu hình trụ
Tính thể tích của một thùng dầu hình trụThể tích của khối trụ được áp dụng trong nhiều tình huống thực tế để tính toán không gian chứa đựng, lượng vật liệu cần thiết, và thiết kế các công trình, thiết bị. Dưới đây là một số ví dụ minh họa cách thể tích của khối trụ được áp dụng trong thực tế:
Tính thể tích bể chứa nước và dầu
- Trong ngành công nghiệp và dân dụng, các bể chứa nước hoặc dầu thường có dạng hình trụ. Để xác định lượng chất lỏng có thể chứa được trong bể, chúng ta cần tính thể tích của khối trụ. Ví dụ:
- Bể nước gia đình: Nếu có bể nước hình trụ có đường kính 2 mét và cao 3 mét, thể tích chứa nước sẽ là: V=πr2h=πr^2 h = π x 1^2 x 3 ≈ 9.42m3.
- Bồn chứa dầu: Bồn dầu trong nhà máy hóa chất cần được thiết kế để chứa một lượng dầu nhất định, do đó việc tính toán thể tích là rất quan trọng để tránh tràn hoặc thiếu dung tích.
Thiết kế và xây dựng các công trình kiến trúc
- Trong kiến trúc, các cột trụ bê tông hoặc gạch thường được sử dụng để nâng đỡ các cấu trúc. Việc tính toán thể tích của những cột trụ này rất quan trọng để xác định lượng vật liệu cần thiết:
- Cột trụ bê tông: Nếu một cột trụ bê tông có đường kính 0.5 m và cao 4 m, thể tích cần đổ bê tông là: V=π×(0.25)^2 ×4≈0.785m3.
- Thiết kế silo chứa ngũ cốc: Silo thường có hình trụ, và việc tính toán thể tích giúp xác định lượng ngũ cốc tối đa có thể chứa được, tránh tình trạng quá tải.
Sản xuất và đóng gói
- Thể tích của khối trụ cũng quan trọng trong ngành sản xuất và đóng gói, đặc biệt là đối với các sản phẩm có dạng hình trụ:
- Lon nước ngọt và đồ hộp: Các lon nước ngọt, bia, đồ hộp, hoặc các loại hộp đựng khác thường có hình trụ. Để tối ưu hóa quá trình sản xuất, các nhà máy cần tính toán thể tích của chúng để thiết kế khuôn mẫu, lên kế hoạch sản xuất, và ước tính chi phí nguyên liệu.
- Ống và đường ống: Để vận chuyển chất lỏng hoặc khí, các kỹ sư cần tính toán thể tích của đường ống hình trụ để biết lượng chất có thể lưu thông qua ống trong một thời gian cụ thể.
Giao thông và vận chuyển
- Thể tích của khối trụ còn được áp dụng trong việc tính toán sức chứa của các phương tiện giao thông:
- Bồn chứa nhiên liệu trong xe tải hoặc xe chở xăng dầu: Các bồn này thường có dạng hình trụ và việc tính toán thể tích giúp xác định lượng nhiên liệu có thể chứa và phân bổ khối lượng an toàn khi vận chuyển.
- Bể chứa khí đốt: Các bồn chứa khí tự nhiên (LPG, LNG) trên tàu hoặc xe bồn cần tính toán thể tích để biết lượng khí tối đa có thể chứa, đảm bảo an toàn và hiệu quả khi vận chuyển.
Y tế và dược phẩm
- Trong ngành y tế và dược phẩm, thể tích của khối trụ cũng được áp dụng để tính toán:
- Ống nghiệm và chai lọ đựng thuốc: Các ống nghiệm trong phòng thí nghiệm hoặc các chai lọ đựng thuốc dạng hình trụ. Việc biết thể tích giúp xác định lượng chất lỏng cần chứa trong các thí nghiệm hoặc khi sản xuất thuốc.
- Máy MRI (Cộng hưởng từ hạt nhân): Phần lõi của máy MRI có dạng hình trụ, và thể tích này cần được tính toán để đảm bảo máy có thể quét toàn bộ cơ thể bệnh nhân.
Khoa học môi trường và nông nghiệp
- Trong lĩnh vực môi trường và nông nghiệp, thể tích của khối trụ được dùng để thiết kế các công cụ và đo đạc:
- Thùng phân compost: Những thùng phân có dạng hình trụ giúp tính toán thể tích để biết lượng phân cần chuẩn bị.
- Lưu trữ và quản lý nước mưa: Bể chứa nước mưa trong các trang trại nông nghiệp thường có dạng hình trụ. Việc tính toán thể tích giúp dự đoán lượng nước có thể thu thập và lưu trữ.
Hệ thống cấp nước và thoát nước
- Thể tích của khối trụ rất quan trọng trong việc tính toán đường ống cấp nước, thoát nước, và xử lý nước thải:
- Thiết kế đường ống thoát nước: Đường ống thoát nước hoặc cống hình trụ yêu cầu tính toán thể tích để đảm bảo đủ lưu lượng thoát nước khi mưa lớn hoặc hệ thống ngập úng.
- Thể tích của khối trụ được sử dụng rộng rãi trong đời sống và sản xuất, từ thiết kế, xây dựng đến quản lý và bảo trì hệ thống. Tính toán chính xác thể tích giúp tối ưu hóa chi phí, tăng cường an toàn và hiệu quả trong nhiều lĩnh vực khác nhau.
.Để nhận được tư vấn về các dịch vụ do HD Home cung cấp, vui lòng liên hệ qua Hotline: 024 62 733 721 hoặc Email: thietkethicongntdhomes@gmail.com để nhận được tư vấn trực tiếp từ phía chuyên viên.