Công thức đạo hàm

1.Đạo hàm là gì?

2.Công thức đạo hàm cơ bản là gì?

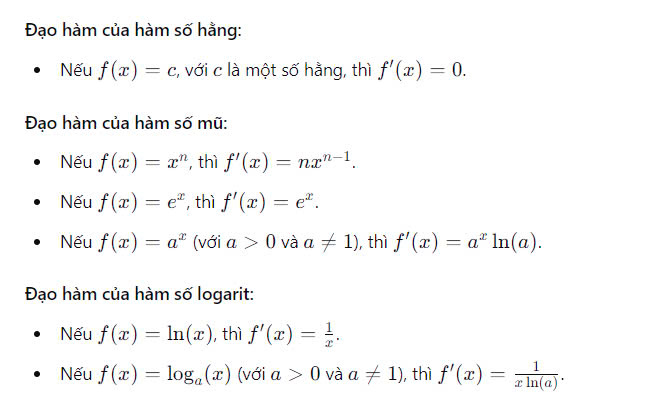
Các công thức tính đạo hàm

3.Các phương pháp để tính đạo hàm

• Sử dụng Định Nghĩa Đạo Hàm: Tính đạo hàm bằng cách áp dụng định nghĩa cơ bản của đạo hàm, là giới hạn của tỷ lệ thay đổi của hàm số khi biến độc lập thay đổi một lượng rất nhỏ.
• Quy Tắc Cơ Bản: Áp dụng các quy tắc cơ bản để tính đạo hàm của các hàm số phổ biến như hàm số mũ, logarit, và hàm lượng giác.
• Quy Tắc Tổng và Hiệu: Tính đạo hàm của tổng (hoặc hiệu) hai hàm số bằng cách tính đạo hàm của từng hàm số riêng lẻ và cộng (hoặc trừ) các kết quả.
• Quy Tắc Tích và Phân: Tính đạo hàm của tích hai hàm số hoặc phân của hai hàm số bằng cách sử dụng quy tắc để kết hợp đạo hàm của các hàm số đó.
• Quy Tắc Chuỗi: Tính đạo hàm của hàm số hợp bằng cách sử dụng quy tắc chuỗi, kết hợp đạo hàm của hàm ngoài với đạo hàm của hàm bên trong.
• Đạo Hàm Bậc Cao: Tính đạo hàm của hàm số bằng cách lấy đạo hàm của đạo hàm, để tìm đạo hàm bậc cao hơn.
• Đạo Hàm Của Hàm Số Đảo: Tính đạo hàm của các hàm số ngược (như hàm lượng giác ngược) bằng cách áp dụng quy tắc đặc biệt cho chúng.
• Kỹ Thuật Tinh Vi Hơn: Sử dụng các kỹ thuật phân tích để tính đạo hàm của các hàm số phức tạp hơn khi các phương pháp cơ bản không áp dụng được.
• Phần Mềm Toán Học: Sử dụng phần mềm hoặc công cụ toán học trực tuyến để tính đạo hàm của các hàm số phức tạp.

Phương pháp tính đạo hàm

4. Ứng dụng của đạo hàm

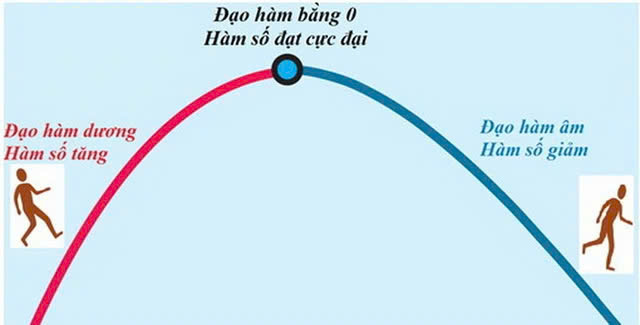
Tìm Cực Trị của Hàm Số

• Mục đích: Tìm các điểm cực đại và cực tiểu của hàm số.
• Cách thực hiện: Tính đạo hàm của hàm số và giải phương trình đạo hàm bằng 0 để tìm các điểm nghi ngờ.
• Xác định loại cực trị (cực đại, cực tiểu hay điểm yên ngựa) bằng cách sử dụng đạo hàm cấp hai (quy tắc đạo hàm cấp hai) hoặc xét sự thay đổi dấu của đạo hàm cấp nhất.
• Ứng dụng: Tối ưu hóa sản xuất, xác định điểm cân bằng trong kinh tế, tìm kiếm thiết kế tốt nhất trong kỹ thuật.

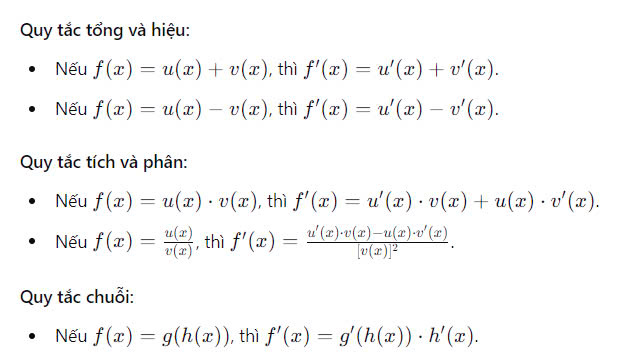
Ứng dụng của đạo hàm

Tính Toán Vận Tốc và Gia Tốc

• Mục đích: Xác định tốc độ và sự thay đổi tốc độ của một vật thể.
• Cách thực hiện: Vận tốc là đạo hàm của hàm số vị trí theo thời gian: v(t)= d/dt.x(t)
• Gia tốc là đạo hàm của hàm số vận tốc theo thời gian: a(t)= d/dt.v(t)
• Ứng dụng: Trong cơ học, điều khiển phương tiện giao thông, phân tích chuyển động trong robot.

Giải Phương Trình Vi Phân

• Mục đích: Mô hình hóa các hệ thống động học và giải quyết các vấn đề liên quan đến sự thay đổi liên tục.
• Cách thực hiện: Phương trình vi phân là phương trình có chứa đạo hàm của hàm số. Giải phương trình vi phân giúp tìm hàm số mà khi đạo hàm của nó thay đổi theo một cách cụ thể.
• Sử dụng các phương pháp như phương pháp Euler, phương pháp Runge-Kutta để giải các phương trình vi phân.
• Ứng dụng: Mô hình hóa sự thay đổi trong tài chính, dự đoán biến động thời tiết, mô hình hóa động học trong vật lý và kỹ thuật.

Ứng dụng của đạo hàm

Tính Toán Độ Dốc và Tiếp Tuyến

• Mục đích: Xác định độ dốc của đồ thị hàm số tại một điểm.
• Cách thực hiện: Đạo hàm tại một điểm cho biết độ dốc của tiếp tuyến tại điểm đó.
• Sử dụng để xấp xỉ giá trị của hàm số gần điểm đó bằng cách sử dụng tiếp tuyến.
• Ứng dụng: Phân tích hình học của hàm số, thiết kế đường cong trong đồ họa máy tính, và kiểm tra các điểm gãy hoặc điểm chuyển tiếp trong dữ liệu.

Tối Ưu Hóa trong Kinh Tế

• Mục đích: Tìm giá trị tối ưu cho các hàm lợi nhuận, chi phí, hay doanh thu.
• Cách thực hiện: Sử dụng đạo hàm để tìm điểm tối đa hoặc tối thiểu của các hàm số mô tả lợi nhuận hoặc chi phí.
• Áp dụng các phương pháp tối ưu hóa như phương pháp gradient descent trong các mô hình kinh tế phức tạp.
• Ứng dụng: Tối ưu hóa chiến lược giá, tối ưu hóa chi phí sản xuất, phân tích điểm cân bằng trong kinh doanh.

Phân Tích Độ Nhạy và Dự Đoán

• Mục đích: Đánh giá sự nhạy cảm của hệ thống đối với các thay đổi trong đầu vào.
• Cách thực hiện: Tính toán đạo hàm để đánh giá sự thay đổi của hàm số đầu ra khi thay đổi các biến đầu vào.
• Sử dụng phân tích độ nhạy để dự đoán hành vi của hệ thống trong các điều kiện khác nhau.
• Ứng dụng: Phân tích rủi ro tài chính, dự đoán phản ứng của hệ thống kỹ thuật, tối ưu hóa hệ thống sản xuất.

Kỹ Thuật Điều Khiển

• Mục đích: Thiết kế và phân tích các bộ điều khiển để hệ thống phản ứng nhanh chóng và chính xác.
• Cách thực hiện: Sử dụng đạo hàm để thiết kế các bộ điều khiển PID (Proportional-Integral-Derivative) mà điều chỉnh hệ thống dựa trên độ dốc và thay đổi của biến điều khiển.
• Phân tích hệ thống động học và điều chỉnh các tham số điều khiển để tối ưu hóa hiệu suất.
• Ứng dụng: Điều khiển robot, hệ thống tự động trong sản xuất, điều khiển phương tiện giao thông.

Hàm Số và Số Học

• Mục đích: Phân tích và tính toán các hàm số phức tạp, giải phương trình.
• Cách thực hiện: Sử dụng đạo hàm để giải phương trình phi tuyến thông qua phương pháp Newton-Raphson, trong đó đạo hàm của hàm số giúp cải thiện các xấp xỉ của nghiệm.
• Ứng dụng: Giải quyết các bài toán số học phức tạp, phân tích dữ liệu khoa học, thiết kế thuật toán trong máy tính.

Tính Toán trong Máy Học và Trí Tuệ Nhân Tạo

• Mục đích: Huấn luyện và tối ưu hóa mô hình học máy.
• Cách thực hiện: Đạo hàm được sử dụng trong các thuật toán tối ưu hóa như gradient descent để điều chỉnh các tham số của mô hình học máy.
• Đạo hàm của hàm mất mát (loss function) giúp cập nhật trọng số và cải thiện hiệu suất của mô hình.
• Ứng dụng: Huấn luyện mạng nơ-ron, tối ưu hóa mô hình dự đoán, phân tích dữ liệu lớn.