Thể tích khối trụ
Công thức tính thể tích của khối trụ là:
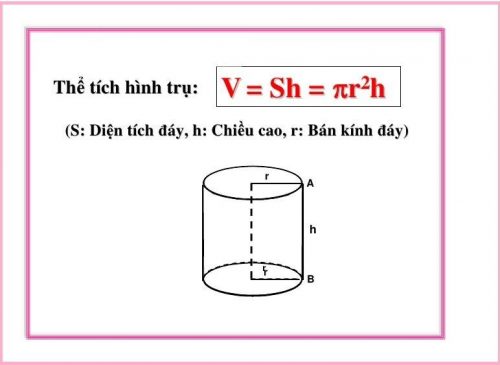
Công thức tính thể tích
Trong đó
V là thể tích của khối trụ.
π (pi) là hằng số toán học khoảng 3.14159.
r là bán kính của mặt đáy hình tròn của khối trụ.
h là chiều cao của khối trụ.
Để tính thể tích khối trụ, bạn chỉ cần thay giá trị của bán kính và chiều cao vào công thức và thực hiện các phép tính cần thiết.
Dưới đây là các khái niệm cơ bản về hình trụ, mặt trụ, và khối trụ:
Hình trụ (Cylinder):
Định nghĩa: Hình trụ là một hình không gian ba chiều có hai mặt đáy hình tròn và một mặt cong bao quanh chúng. Các mặt đáy của hình trụ là hai mặt tròn bằng nhau và song song với nhau.
Đặc điểm: Mặt cong của hình trụ là một hình chữ nhật hoặc hình elip khi được cắt theo mặt phẳng vuông góc với trục hình trụ.
Mặt trụ (Lateral Surface of a Cylinder):
Định nghĩa: Mặt trụ là phần mặt bên của hình trụ, không bao gồm các mặt đáy. Mặt này có hình dạng giống như một hình chữ nhật hoặc hình elip khi hình trụ được mở ra.
Diện tích mặt trụ: Công thức tính diện tích mặt trụ là:
Amặt trụ =2πrh Trong đó:
𝑟
r là bán kính của mặt đáy hình tròn.
ℎ
h là chiều cao của hình trụ.
Khối trụ (Solid Cylinder):
Định nghĩa: Khối trụ là hình trụ hoàn chỉnh, bao gồm cả hai mặt đáy và mặt bên. Đây là hình không gian ba chiều với hai mặt đáy tròn và một mặt bên cong.
Thể tích khối trụ: Công thức tính thể tích của khối trụ là:
V=πr
2
h Trong đó:
𝑟
r là bán kính của mặt đáy.
ℎ
h là chiều cao của khối trụ.
Những khái niệm này giúp bạn hình dung và tính toán các đặc điểm của hình trụ trong không gian ba chiều.
Hình dáng khối trụ
Công thức toán học có nhiều ứng dụng thực tiễn trong đời sống hàng ngày. Dưới đây là một số ví dụ:
Tính toán chi phí và ngân sách: Công thức tính phần trăm giúp bạn quản lý ngân sách và chi tiêu hiệu quả. Ví dụ, khi bạn giảm giá một sản phẩm, bạn có thể sử dụng công thức tính phần trăm giảm giá để biết số tiền bạn cần trả.
Xây dựng và thiết kế: Các công thức tính thể tích khối trụ theo hình học và đại số được sử dụng trong xây dựng và thiết kế để tính diện tích, thể tích và các kích thước cần thiết. Ví dụ, khi xây dựng một ngôi nhà, bạn cần tính diện tích của các phòng để lựa chọn số lượng vật liệu xây dựng.
Y tế và sức khỏe: Các công thức toán học được sử dụng để tính chỉ số khối cơ thể (BMI), liều lượng thuốc dựa trên trọng lượng cơ thể, hoặc tỷ lệ phần trăm mỡ cơ thể.
Khoa học và kỹ thuật: Công thức hóa học và vật lý là cơ sở để hiểu các quá trình tự nhiên và kỹ thuật. Ví dụ, các công thức trong động lực học giúp thiết kế và kiểm tra các phương tiện giao thông.
Tài chính và đầu tư: Công thức lãi suất đơn, lãi suất kép, và các công thức tài chính khác giúp tính toán lợi nhuận đầu tư, tiết kiệm, và quản lý tài sản.
Giao thông và du lịch: Công thức tính thời gian và khoảng cách giúp lập kế hoạch cho chuyến đi và ước lượng thời gian di chuyển giữa các điểm đến.
Những ứng dụng này cho thấy công thức không chỉ là lý thuyết mà còn là công cụ hữu ích trong nhiều lĩnh vực của cuộc sống hàng ngày.
cách ghi nhớ thể tích khối trụ
Để ghi nhớ thể tích của khối trụ mà không cần phải nhớ công thức cụ thể, bạn có thể sử dụng một số phương pháp gợi nhớ sau:

Ứng dụng của khối trụ trong xây dựng
Hình ảnh và So sánh:
Hình Trụ: Tưởng tượng một hộp hình trụ, như hộp sữa hoặc chai nước. Để tính thể tích, bạn cần biết hai yếu tố: diện tích đáy và chiều cao.
Diện Tích Đáy: Diện tích đáy là diện tích của mặt tròn dưới cùng, tương tự như việc tính diện tích của một chiếc đĩa tròn.
Lưu Ý Cấu Trúc:
Diện Tích Đáy: Nhớ rằng để tính thể tích, bạn cần nhân diện tích đáy với chiều cao của hình trụ. Diện tích đáy là hình tròn, và bạn có thể tưởng tượng việc nhân diện tích của một cái đĩa tròn với độ cao của hộp.
Chiều Cao: Tưởng tượng độ cao của hình trụ như chiều cao của hộp hoặc chai.
Gợi Nhớ Bằng Ví Dụ:
Ví dụ Hộp Đựng: Hãy tưởng tượng bạn có một hộp hình trụ với đáy là một cái đĩa tròn. Để biết được tổng thể tích của hộp, bạn cần biết phần diện tích đáy (cái đĩa) và nhân với chiều cao của hộp.
Kết Hợp Tưởng Tượng:
Hình Tròn Nhân Chiều Cao: Hãy nhớ rằng thể tích là "diện tích của mặt đáy nhân với chiều cao". Nếu hình trụ là một chai nước, thể tích chính là diện tích mặt đáy (phần tròn) nhân với chiều cao của chai.
Bằng cách sử dụng các phương pháp gợi nhớ này, bạn có thể dễ dàng nhớ được cách tính thể tích của khối trụ mà không cần phải nhớ công thức cụ thể.