Công thức đạo hàm
Đạo hàm là một khái niệm cơ bản trong giải tích toán học, được sử dụng để mô tả sự thay đổi của một hàm số khi biến số đầu vào của hàm thay đổi. Đạo hàm của một hàm số tại một điểm cụ thể cho biết tốc độ thay đổi của hàm số đó tại điểm đó.
Ý Nghĩa Đạo Hàm
Tốc Độ Thay Đổi: Đạo hàm cho biết tốc độ thay đổi của hàm số tại một điểm cụ thể. Nếu hàm số mô tả vị trí của một vật trong thời gian, thì đạo hàm của hàm số đó tại một thời điểm cụ thể chính là vận tốc của vật tại thời điểm đó.
Đường Tiếp Tuyến: Đạo hàm tại một điểm cũng có thể được hiểu là hệ số góc của đường tiếp tuyến với đồ thị của hàm số tại điểm đó.
Tính Đạo Hàm
Đạo hàm có thể được tính bằng cách sử dụng các quy tắc và phương pháp khác nhau, bao gồm:
Quy Tắc Đạo Hàm: Quy tắc cơ bản như quy tắc đạo hàm của tổng, tích, thương của hai hàm số, và quy tắc chuỗi.
Đạo Hàm Của Các Hàm Cơ Bản: Đạo hàm của các hàm số cơ bản như hàm số mũ, hàm số lượng giác, và hàm số logarit.

Quy tắc dạo hàm cơ bản

Công thức sơ cấp
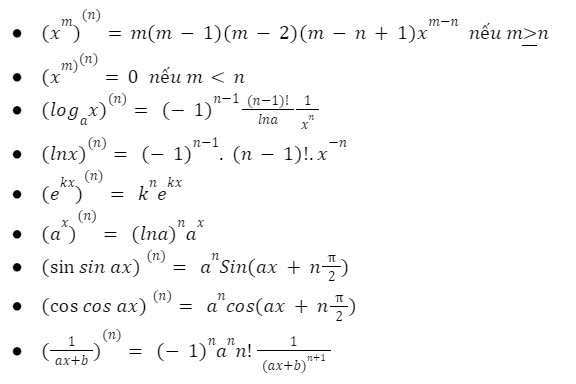
Công thức Đạo hàm cấp cao
Công thức đạo hàm không chỉ là một phần quan trọng trong toán học mà còn có nhiều ứng dụng thiết thực trong đời sống và các lĩnh vực khác nhau. Dưới đây là một số ứng dụng phổ biến của công thức :
Vật Lý
Tốc Độ và Gia Tốc: Đạo hàm của vị trí theo thời gian cho biết tốc độ của một vật, trong khi đạo hàm của tốc độ cho biết gia tốc. Ví dụ, trong chuyển động của một chiếc xe, đạo hàm của hàm vị trí theo thời gian cho biết vận tốc và đạo hàm của vận tốc cho biết gia tốc.
Lực và Công: Trong cơ học, đạo hàm của động năng theo thời gian có thể cho biết công suất, và đạo hàm của lực theo thời gian có thể cho biết sự thay đổi của lực tác động.
Kinh Tế
Tối Ưu Hóa: Đạo hàm được sử dụng để tìm điểm tối ưu trong các bài toán tối ưu hóa, chẳng hạn như tối đa hóa lợi nhuận hoặc tối thiểu hóa chi phí. Đạo hàm giúp xác định các điểm cực trị của hàm lợi nhuận hoặc hàm chi phí.
Phân Tích Xu Hướng: Đạo hàm giúp phân tích sự thay đổi trong các yếu tố kinh tế như giá cả, doanh thu, và sản lượng. Ví dụ, đạo hàm của hàm doanh thu theo số lượng sản phẩm cho biết sự thay đổi trong doanh thu khi số lượng sản phẩm thay đổi.

Đạo hàm ứng dụng và nhiều lĩnh vựcKỹ Thuật và Khoa Học
Thiết Kế Cơ Cấu và Hệ Thống: Trong kỹ thuật, đạo hàm giúp thiết kế và phân tích các cơ cấu và hệ thống, chẳng hạn như hệ thống điều khiển tự động, bằng cách xác định các yếu tố như tốc độ và phản ứng của hệ thống.
Mô Hình Hóa và Dự Đoán: Đạo hàm được sử dụng trong các mô hình toán học để dự đoán các hiện tượng trong khoa học, chẳng hạn như sự phát triển của bệnh dịch hoặc sự thay đổi của các yếu tố môi trường.
Tài Chính
Định Giá Quyền Chọn: Trong tài chính, đạo hàm được sử dụng để định giá các quyền chọn và hợp đồng tài chính. Các mô hình định giá quyền chọn như mô hình Black-Scholes sử dụng đạo hàm để tính toán giá trị của quyền chọn.
Phân Tích Rủi Ro: Đạo hàm giúp phân tích và quản lý rủi ro trong đầu tư tài chính, chẳng hạn như xác định độ nhạy cảm của một khoản đầu tư đối với các yếu tố thị trường.
Sinh Học và Y Học
Mô Hình Sinh Trưởng: Trong sinh học, đạo hàm được sử dụng để mô hình hóa sự phát triển của các loài, sự thay đổi của số lượng tế bào, và các hiện tượng sinh học khác.
Phân Tích Dữ Liệu Y Học: Đạo hàm giúp phân tích dữ liệu y học để hiểu rõ hơn về sự thay đổi của các chỉ số sức khỏe theo thời gian và xác định xu hướng của các bệnh lý.
Định Tuyến và Quy Hoạch
Lập Kế Hoạch và Quản Lý Dự Án: Đạo hàm giúp tối ưu hóa các kế hoạch và dự án, chẳng hạn như tối ưu hóa lịch trình làm việc hoặc phân bổ tài nguyên.
Tối Ưu Hóa Quy Trình: Trong công nghiệp, đạo hàm được sử dụng để tối ưu hóa quy trình sản xuất, giảm thiểu thời gian sản xuất, và tăng hiệu quả sử dụng nguyên liệu.
Học Máy và AI
Huấn Luyện Mô Hình: Trong học máy và trí tuệ nhân tạo, đạo hàm được sử dụng để cập nhật trọng số của các mô hình học máy trong quá trình huấn luyện. Ví dụ, trong thuật toán lan truyền ngược (backpropagation), đạo hàm giúp điều chỉnh các trọng số để cải thiện độ chính xác của mô hình.
Như vậy, công thức đạo hàm có ứng dụng rộng rãi trong nhiều lĩnh vực, giúp giải quyết các vấn đề phức tạp, phân tích sự thay đổi, và tối ưu hóa các quá trình.